本科时的课设

设计并实现一个数据挖掘软件系统：使用Python语言，读取数据集文件中的数据，对数据进行数据挖掘算法解析。算法可选用ID3或C4.5分类算法。

输入：数据集，所有特征名

输出：决策树

输入：需要分类的数据

输出：分类结果

系统提供命令行交互模式和UI窗口模式两种操作方式，前者基于Python命令行，后者使用PyQt5做底层支持。

本系统在Windows平台下开发，编写可执行的Python脚本软件，主要分为ID3算法脚本、C4.5算法脚本，数据集测试脚本和UI脚本。

ID3算法脚本

1. 首先检测所有的属性，选择信息增益最大的属性产生决策树结点，由该属性的不同取值建立分支。

2. 再对各分支的子集递归调用该方法建立决策树结点的分支，直到所有子集仅包含同一个类别的数据为止。

3. 最后得到一棵决策树，它可以用来对新的样本进行分类。

C4.5算法脚本

1. 首先检测所有的属性，选择信息增益率最大的属性产生决策树结点，连续型属性数据和离散型属性数据分开处理，由该属性的不同取值建立分支。

2. 再对各分支的子集递归调用该方法建立决策树结点的分支，直到所有子集仅包含同一个类别的数据为止。

3. 最后得到一棵决策树，它可以用来对新的样本进行分类。

数据集测试脚本

UI脚本

伪代码

划分数据集，我们遵循以下原则：如果某个分支的数据属于同一类型，则无需进一步对数据进行划分；如果数据子集内的数据不属于同一类型，则需要重复划分数据子集的过程。

划分数据集前后信息发生的变化称为信息增益，著名的ID3决策树算法就是以信息增益为准则的。香农熵是度量信息增益的的一种常用度量方法（度量信息无序程度有两种方法，除了香农熵之外就是基尼不纯度，CART决策树就是使用"基尼指数"来选择划分属性）

最重要的是搞清楚几个概念：

数据集：数据集合

特征（属性）：即横向的key名

分类值（属性值）：即纵向的value值

类别：即分支

类型：分类后最后得到结果，确认yes or no

有个特点，每次都是根据-1最后一列的值，来决定如何分类的

连续属性离散化

C4.5算法中策略是采用二分法将连续属性离散化处理：假定样本集D的连续属性有n个不同的取值，对这些值从小到大排序，得到属性值的集合。把区间的中位点作为候选划分点，于是得到包含n-1个元素的划分点集合

基于每个划分点t，可将样本集D分为子集和，其中中包含属性上不大于t的样本，包含属性上大于t的样本。

对于每个划分点t，按如下公式计算其信息增益值，然后选择使信息增益值最大的划分点进行样本集合的划分。

calcShannonEnt 公式1

chooseBestFeatureToSplit 公式2，得到最佳特征

majorityCnt

基于最好的特征值划分数据集，由于属性值可能多于一个，因此可能存在大于两个分支的数据集划分。

第一次划分后数据将被向下传递到树分支的下一个结点，在这个结点上，我们可以再次划分数据。这很明显是个递归的过程。那么递归算法的临界条件是：程序遍历完所有划分数据集的属性，或者每个分支下的所有实例都具有相同的分类。

如果当程序遍历完所有划分数据集的属性，但是当前叶子结点的类标签依然不是唯一的，此时我们就采用以前一篇博客：K近邻算法讲解与python实现（附源码demo下载链接）中采用的投票表决方法

def calcShannonEnt(dataSet):统计所有类别标签的发生频率然后计算类别出现的概率–香农熵，返回熵值。

为所有的分类类目创建字典,key为label数据，value为count，存储出现的次数。再根据公式计算香农熵

def splitDataSet(dataSet, axis, value):按照某个特征进行数据集划分，参数三个变量分别是待划分的数据集，特征，分类值。返回不含划分特征的子集。

遍历数据集，找到特征值为value的数据，将特征值从数据集中排除，最后返回不含划分特征的子集。

def chooseBestFeatureToSplit(dataSet):寻找最佳特征，按照最大信息增益划分数据。返回特征值。

遍历数据集中的所有特征，得到某个特征下所有值，存为list，再保存为set。遍历当前特征中所有的唯一属性值，对每个特征划分的属性值进行熵求和，对各子集香农熵求和。用公式计算信息增益，记录最大信息增益，返回对应的特征值。

def majorityCnt(classList):投票表决代码

如果当程序遍历完所有划分数据集的属性，但是当前叶子结点的类标签依然不是唯一的，此时我们就采用投票表决方法。

此时所有的特征都被用上过，列表里只剩下了label，树的构建中终止，但是这个叶子数据集里所有的数据还是有不同的label，这时就要用服从多数

def createTree(dataSet, labels):构建决策树，返回决策树。

抽取数据集分类值作为一个list，类别相同，停止划分；或长度为1，投票表决，返回出现次数最多的类别

按照信息增益最高选取分类特征属性，得到分类的特征序号，该特征的label，构建树的字典，从labels的list中删除该label，最后构建数据的子集合，并进行递归。最终得到决策树，返回。

def classify(inputTree, featLabels, testVec):分类。程序比较测试数据与决策树上的数值，递归执行该过程直到进入叶子结点；最后将测试数据定义为叶子结点所属的类型。三个变参数是决策树，属性特征标签，测试的数据。返回最终的类别。

在原有ID3算法上改进：

def splitDataSet_c(dataSet, axis, value, LorR='L'):划分数据集, axis:按第几个特征划分, value:划分特征的值, LorR: value值左侧（小于）或右侧（大于）的数据集。

因为要处理连续型数据，因此我们要引入比较计算。

def chooseBestFeatureToSplit_c(dataSet, labelProperty):修改原来的最优划分属性选择方法，在其中增加连续属性的分支。

处理连续值的策略是采用二分法将连续属性离散化处理：假定样本集D的连续属性有n个不同的取值，对这些值从小到大排序，得到属性值的集合。把区间的中位点作为候选划分点，于是得到包含n-1个元素的划分点集合。基于每个划分点t，可将样本集D分为子集和，其中中包含属性上不大于t的样本，包含属性上大于t的样本。对于每个划分点t，按公式计算其信息增益值，然后选择使信息增益值最大的划分点进行样本集合的划分。

def createTree_c(dataSet, labels, labelProperty):修改原来的决策树构建方法，增加参数特征属性（0表示离散，1表示连续），对连续的特征，不删除该特征，分别构建左子树和右子树

def classify_c(inputTree, featLabels, featLabelProperties, testVec):修改原来的测试方法，同样对于连续型数据做不同处理，如左右子树的选择。

def openDataSet(path):打开路径为path的数据集文件，从文件中读取数据集中的数据，根据数据格式的不同，进行预处理，转为Python内置类型并返回。

def chooseCreateTree(algorithm, dataSet, labels, labelProperties):可选择调用ID3算法脚本或C4.5算法，构建决策树，然后即可根据决策树进行分类。

def chooseClassify(algorithm: str, tree, labels, labelProperties, testVec): 可选择调用ID3算法脚本或C4.5算法，提供决策树和测试数据，返回分类结果。

def setupUi(self, MainWindow): UI初始化，设置UI各个子元件。

def __init__(self, parent=None): 设置一些默认参数。

def selectfile(self): 选择文件功能的实现。还有一些其他UI功能的实现略。

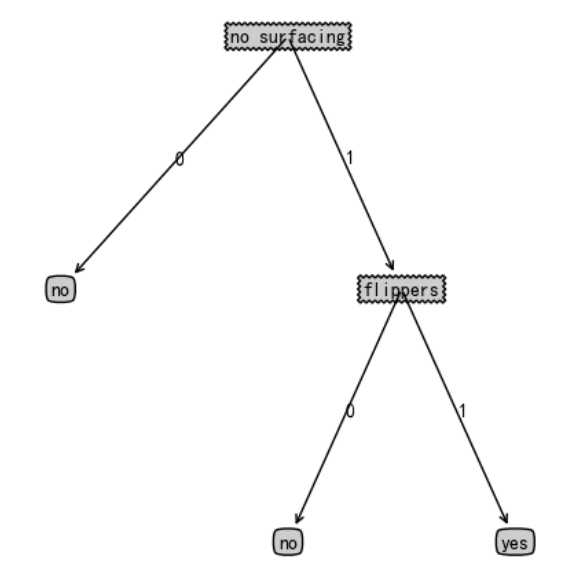
树：{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}

急性炎症数据集

ID3的决策树

{'Temperature': {'36': 'no', '40': {'Lumbar pain': {'yes': 'yes', 'no': 'no'}}, '35': 'no', '39': 'yes', '38': 'yes', '41': {'Lumbar pain': {'yes': 'yes', 'no': 'no'}}, '37': 'no'}}

C4.5的决策树

{'Temperature<37.5': {'是': 'no', '否': {'Lumbar pain': {'yes': 'yes', 'no': 'no'}}}}

测试分类数据

[37, 'no', 'no', 'yes', 'yes', 'yes', 'yes'] 结果：no

[37, 'no', 'no', 'no', 'no', 'no', 'no'] 结果：no

[41, 'yes', 'yes', 'no', 'yes', 'no', 'no'] 结果：yes

全部正确

鸢尾花数据集

因ID3不支持连续型数据，因此无法用ID3解析

C4.5的决策树

{'petal length<2.45': {'是': 'Iris-setosa', '否': {'petal width<1.75': {'是': {'petal length<4.95': {'是': {'petal width<1.65': {'是': 'Iris-versicolor', '否': 'Iris-virginica'}}, '否': {'petal width<1.55': {'是': 'Iris-virginica', '否': {'sepal length<6.95': {'是': 'Iris-versicolor', '否': 'Iris-virginica'}}}}}}, '否': {'petal length<4.85': {'是': {'sepal length<5.95': {'是': 'Iris-versicolor', '否': 'Iris-virginica'}}, '否': 'Iris-virginica'}}}}}}

测试分类数据

[5.4, 3.9, 1.7, 0.4] 结果：Iris-setosa

[6.4, 2.9, 4.3, 1.3] 结果：Iris-versicolor

[6.3, 2.7, 4.9, 1.8] 结果：Iris-virginica

全部正确

使用Python3.7解释器执行脚本，然后即可调用API接口，以参数形式输入，返回值输出结果

主要的接口：

DataSetTest.openDataSet(path) 打开数据集文件，需要提供路径

DataSetTest.chooseCreateTree(algorithm, dataSet, labels, labelProperties) 选择构建树算法

DataSetTest.chooseClassify(algorithm: str, tree, labels, labelProperties, testVec) 选择算法并分类

使用示例：

命令行模式

Python 3.7.0 (v3.7.0:1bf9cc5093, Jun 27 2018, 04:59:51) [MSC v.1914 64 bit (AMD64)] on win32

输入以下命令，即可以交互模式显示结果

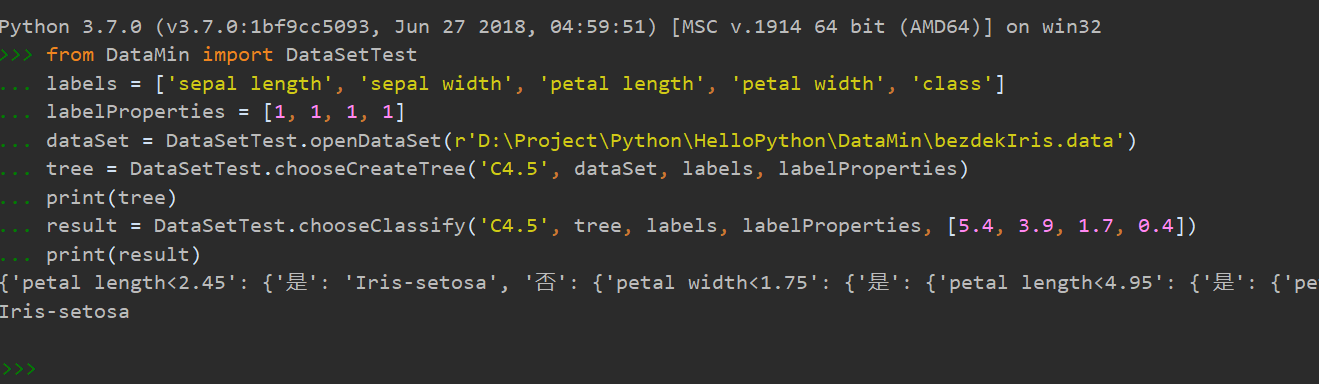
from DataMin import DataSetTest

labels = ['sepal length', 'sepal width', 'petal length', 'petal width', 'class']

labelProperties = [1, 1, 1, 1]

dataSet = DataSetTest.openDataSet(r'D:\Project\Python\HelloPython\DataMin\bezdekIris.data')

tree = DataSetTest.chooseCreateTree('C4.5', dataSet, labels, labelProperties)

print(tree)

result = DataSetTest.chooseClassify('C4.5', tree, labels, labelProperties, [5.4, 3.9, 1.7, 0.4])

print(result)

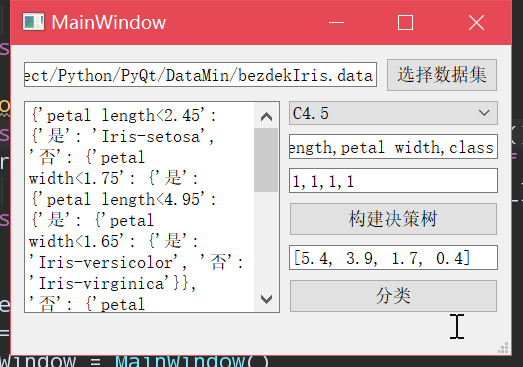
UI窗口模式

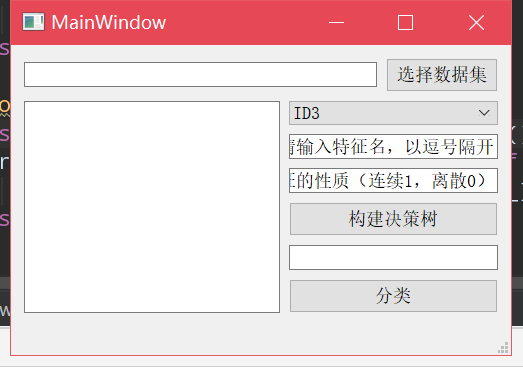
首先点击"选择数据集"，会弹出文件选择窗口

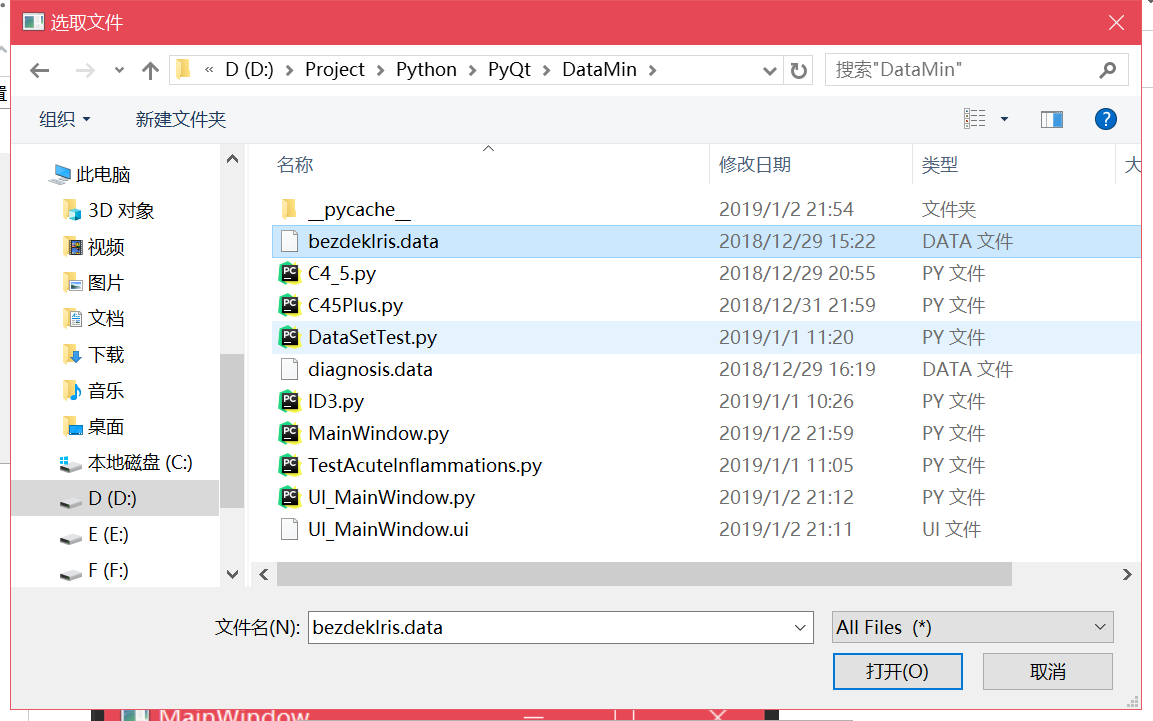
选择一个数据集。

然后在右边的控件中选择要执行的分类算法，再依次输入所有特征名，以及是离散还是连续的（1表示连续，0表示离散）。

点击"构建决策树"，即在左侧显示构建出的决策树

最后，输入要分类的数据，点击"分类"，即可在左侧显示分类结果

本次数据挖掘大作业，我完成了包含ID3和C4.5两个分类算法的软件系统，并用该系统完成了急性炎症和鸢尾花两个数据集的解析，最后测试的分类结果也都是正确的。

在实现的过程中，我参考了书本和网络等来源的资料，对于数据挖掘的具体实现和运用有了一个初体验，并认识到这门学科的重要性和实用性。通过实际的代码编写和调试，我感受到数据挖掘算法的强大和精妙。

这次我完成的算法只是数据挖掘算法中最基础的部分，后面还有非常多的知识等待我们去探索，我们所需要解决的难点也会增多，往后我会继续学习，感受计算机科学博大精深。

蒋盛益《数据挖掘原理和实践》

柴玉梅《人工智能》

周志华《机器学习》

J.Ross Quinlan C4.5: Programs For Machine Learning