A*寻路算法的改进及其在游戏中的运用
摘要:在游戏人工智能中,角色的智能寻路系统一直是研究的重点。目前电子游戏使用的智能寻路算法中最为经典的是 A*算法,其它很多优秀的寻路算法也都是从该算法中发展而来。但是标准的 A*算法也存在着一些不足。本文通过对标准A*算法详细研究,提出了几种优化方法来对其进行改进:用二叉堆对列表数据结构进行优化,启发函数添加系数优化,路径权值优化,分区域搜索优化。采用上述几种方法改进优化标准的 A*算法后,寻路效率更高、使用范围更广、玩家体验更好,且可以实际应用在游戏中。
关键词:人工智能;寻路系统;A*算法;游戏开发
一、引言
从上个世纪六十年代初开始电子游戏的出现到而今,电子游戏产业取得了极大的成长。现在的电子游戏有着丰富的图形图像、更加真实的物理模拟引擎、良好的互动性和逼真的人工智能。当今社会计算机的快速发展,使得电子游戏逐渐被社会所认可,由于其交互性强,能够让玩家产生身临其境的沉浸感,在日常生活中作为一个不可忽视的娱乐项目,慢慢成为一种特别的艺术形式。计算机硬件的发展成熟,使得电子游戏画面、模型等方面逐渐遇到发展瓶颈,而在与人的互动性上却还有很大潜力,人工智能在游戏中的地位越来越高,游戏中"高智商"、看起来很"聪明"的机器人往往带给玩家很高的体验感,让玩家感觉到是在和真实的生物互动。
游戏人工智能中的角色模拟人的行动,可以像人一样进行简单"思考",使游戏中的角色更加智能化。游戏人工智能的研究不仅要懂心理学,更要拥有足够的计算机知识,使得"智能"能够在计算机等平台上实现。电子游戏中常见的人工智能有AI(ArtificialIntelligence,中文为人工智能)策略、AI寻路系统、AI战术体系和AI学习等技术,其中AI寻路系统在游戏中,尤其是对拥有"智慧"的角色来说至为重要。一个角色能不能找到一条通往某处的路径,所走路径是否符合人的思维等是一个很难完美实现的功能,也给游戏编程人员带了很大的挑战。
寻路系统中常用到的算法就是A*路径搜索算法,本文重点阐述和研究了该A*算法,并在此算法基础上进行了改进和优化,使其应用在游戏中时,角色寻找到的路径更加符合正常人类思考后的路径。
二、寻路技术基础研究
在电子游戏中,场景是一个游戏的环境,其和人生存的现实世界很相似,场景里面有天空和地形,有江河与森林,有建筑与生物等,对于一个场景中的地图,上述除了天空基本都放在这张地图上,游戏中的角色要想在此地图上进行运动等操作,就应该和现实中一样可以走过某条路、绕过某建筑,游戏的地图常常标注坐标,而角色在地图中行走其实就是在二维或三维坐标世界上不断地移动。要想在游戏地图中实现类似于人在现实中的行走,就要把游戏里的地图模拟到现实中。当前大部分游戏的地图都被划分为了很多小方格(也可以划分为三角格、六角格等),当角色从某一位置准备移动到另一位置时,游戏程序通过己经写好的路径寻找算法计算出合适的路径(路径是一个路径点集合),然后控制角色沿着路径点对应的方格进行一步步位移直到顺利到达目的地。
角色如何快速准确地移动到指定的位置,一直是游戏开发人员所关心和研究的重点之一,采用不同的寻路算法得出的路径也各不相同,甚至找不到通往目的地的路径[}ZO}。游戏角色寻路所采用的算法其实都属于图搜索算法,在此基础上衍生出不同效率不同结果的寻路算法。
2.1图和二维网格
数据结构中的图(Graph)指的是由一系列节点以及连通这些节点的线所组成的一种数据构成。其通用定义为:图G=(V,E)是由顶点的集合V和边的集合E所共同组成。每一条边的两端分别连接着一个顶点,所以边可以写成(m, n),其中m,n∈V。如下图2-1所示,两个均为图,其中左边图的边是没有方向的,也就是说边x既可以用(a, b)来表示,又可以用(b, a)来表示,是没有顺序之分的,这样的图称为无向图;同理,右图边Y为带有方向的点对,边Y(d, e)和z(o, d)不同,带有向边的图被称为有向图。
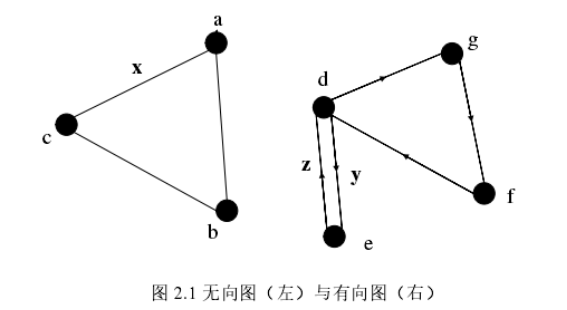
2.2传统寻路算法
2.2.1 Dijkstra算法
Dijkstra(迪杰斯特拉)算法是最为经典的寻路算法。1959年,由荷兰计算机科学家Edsgar Wybe Dijkstra正式提出该算法,该算法从本质上来说是借鉴了贪婪算法的思想,使用它来求解从一个出发点到目标点间的最短路径很简单。该算法的原理就是:标注起始点为中心点,访问完起始点之后,接着访问起始点周围的相邻节点,每次搜索完一个节点都把路径的信息存储在一张表中,之后再向外扩散访问节点的相邻节点,这样层层向外访问,直到访问到目标节点为止。表中存储的长度最短的一组节点集合就是所要寻找的路径。
2.2.2最佳优先搜索算法
最佳优先搜索(BestFirstSearch)算法其实属于启发式的搜索算法的一类。启发式搜索和前面的盲目搜索不同,盲目搜索是按照固定的模式进行搜索,没有目的性、全盘搜索,而启发式搜索则是在寻找路径的过程中,利用一些可以提前计算出的有利信息作为估价值,程序通过估价值提供的信息进行更加智能化的查找。这种通过启发信息来指导整个计算搜索过程的算法,统称为启发式搜索算法。
一般来说,最常用的启发信息便是设置一个估价函数F(n),通过估价函数来引导搜索。最佳优先搜索算法的估价函数是对游戏场景地图中起始点到目标点之间的距离经过简单的估值计算得出一个估价值,该算法与Dijkstra搜索算法的不同之处就是其在选择下一个节点的时候并不是取相邻节点中靠近起始节点的顶点,相反是取相邻节点中靠近目标节点的顶点,这一项改动大大提高了该算法的搜索速度。
2.3标准A*算法
前面两种算法都存在一定的缺陷,在1968年,由PeterHart等几个美国人提出了一种电子游戏中最为经典的路径寻找算法:A*算法。之后对该算法进行的一些微小改动也都统称为A*算法。
A*算法是游戏场景地图中寻找路径时,运用到的最常见的一种。很多智能寻路算法如D*寻路和NavMesh导航网格寻路都是在A*算法基础上产生的。该算法继承了启发式搜索算法的特点,可以在启发信息的引导下生成当前地图中存在的最短路径。
标准A*算法的原理就是借助于开启列表(OpenList)和关闭列表(ClosedList)两个列表,通过估价函数F(n)=G(n)+H(n)来引导整个路径搜索的过程,快速寻找到一条最短的路径。使用标准A*算法进行寻找路径的搜索过程如下:
1)开始设置好起始节点S和目标节点E。之后建立两个空的List:OpenList和ClosedList。
2)取起始节点S并把其放入OpenList中。
3)从OpenList中拿到某节点a,a是根据估价函数找到当前节点到目标节点最小估价值f的节点。
4)把节点a从OpenList中删除并放入到ClosedList中,若节点a即为目标节点E,则证明找到了路径,退出;如果不是,转5。
5)获取到的所有与4中节点a相邻的节点,同理根据启发函数来对这些相邻节点bi的估价值fi进行计算。
6)当相邻节点bi不在OpenList中,且不在ClosedList中,则把节点bi连同起始节点S到其之间的路径信息msg插入OpenList中;当节点bi已经存在于OpenList中,则对比节点bi的已存入和准备存入的估价值f,值小的代替值大的,同时更新msg;如果节点bi已经存在于ClosedList中,则跳过此节点7)循环第3步到第6步,当相邻节点是目标节点或OpenList为空时结束。
具体的标准A*寻路算法的搜索路径过程可以参考流程图所示:
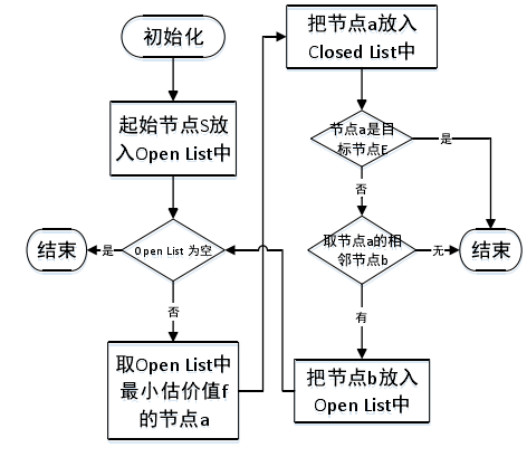
开启列表和关闭列表是A*算法在寻路搜索的过程中必须维护的两张表。开启列表中存放着即将被访问但未被访问的节点,同时这些节点所对应着的估价值也被存放在该表中;而关闭列表中则存放着已经访问完成的节点,而从起始节点到这些完成节点路径信息也都被一同存放在此表中。
对于开启列表来说,每一次计算路径的时候都需要调用到该表,对开启列表执行的操作一般有四个:不断地循环从表中读取到当前估价值最低的节点,读取到之后从该表中删除之;访问相邻节点时首先在该表中检查是否存在于表中;当开启列表里存在此节点,但此节点计算后的估价值比将要插入开启列表中相同节点的估价值要大,则需替换该节点在表中的估价值;访问到新的临近节点并插入到该表中。这四个操作中使用到的寻找、插入和删除操作都是对表的常用操作。
除此之外,启发函数如何选择是A*算法所面临的难点。标准A*算法常采用的曼哈顿距离和切比雪夫距离设置启发函数时,寻路的速度会很快,但是搜索的路径会出现很多相同的路径长度,实际中只需要选择其中一条路径就可以,产生了很多不必要的搜索时间,造成了计算浪费。因此,针对标准A*算法的特点,我们可以对其进行有效的优化。
三、A*寻路算法的改进
3.1 二叉树与二叉堆
二叉树(Binary Tree)是一颗每一个节点至多只允许拥有两个子节点的树。一个完全二叉树指的是除了其最下面一层,其余各层的节点数都达到该层的最大个数,而且最下面一层剩余的所有子节点都连续分布于最下层的0,1,2,3…位置处。
二叉堆是堆的一种较为特别的数据结构,其和完全二叉树有一点类似,然而不同之处在于其除了拥有完全二叉树的所有特性外,父节点总是比其所有子节点的值都要大(或小)。
在本文中,对A*算法优化时所采用的是父节点总是比子节点小的最小堆形式来表示二叉堆。在维护开启列表时,采用数组来表示二叉堆,如下图所示:
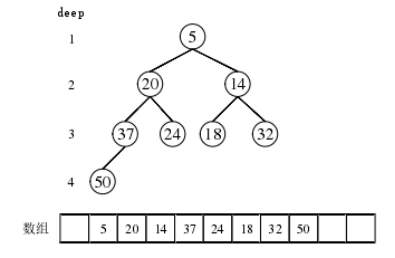
通过数组表示时,根节点在数组 Array 的 Array[1]处。如果把此二叉堆用来表示一个估价值,其中估价值,即路径最短的就在深度为 1 的根节点位置。
3.2 二叉堆节点操作
在维护开启列表时,需要对最小二叉堆进行四种操作,其中查找操作很简单,只能对数组Array从头开始遍历,时间复杂度为O(n)。对于插入节点时,需要区分:如果是新节点且估价值最大,则直接插入到数组的末尾Array[n+1];新节点的估价值在二叉堆中排在靠前位置则要进行类似二叉树的插入操作。如果是已经存在的节点且需要替换时要执行替换操作,则执行先删除再插入操作即可。在执行删除操作时同样用到了类似二叉树的删除方法。插入和删除操作的时间复杂度变为O(log(n))。
3.3 启发函数优化
在较为复杂的游戏地图中,地图上可能有山川、河流、草地、峭壁、沼泽、山洞、房屋等各种地形和建筑,这些地形和建筑抽象到网格地图中就是不同的权值。而使用A*算法中的启发函数来对这些权值进行计算时,如果是角色可以走过的地形,可以在启发函数中对这些可通过地形权值设置和普通地形相近,这样A*算法在使用启发函数进行计算时就不会出现绕很大圈后又回到初始某点计算,再进行绕圈的恶性循环中。而对于山洞这类的凹形明显的地形,则可在启发函数中设置为Blocks,不可通过自动寻路进入。
对于场景地图中的大片连续地形,如果仍然使用未优化过的启发函数来引导搜索过程,则会产生大量相同路径长度的路径,而这样会产生很多不必要的时间损耗,使整个的寻路效率变差。在Heuristics函数中可以加入一个启发系数(HeuristicsFactor)来避免这种情况发生。估价函数F(n)=G(n)+H(n),A*算法中常用的曼哈顿距离和切比雪夫距离所计算出的估价值很有很多重复,通过图可以很直观看出。一般G(n)指的都是起始节点到当前节点的真实路径长度,则可以调节H(n)即启发函数来避免上述情况发生。
本论文采用的优化方法是在每次调用启发函数值时,传入一个当前系统时间的倒数。在H(n)中当前点的权值与启发系数的乘积(即k*t+weight),k为在H(n)中做循环操作时的一个从1开始每次加1的累加器,当k*t>1是,k重置为0继续累加。这样在面对一般的游戏场景地图已经满足,对于更加复杂或巨大的地图则考虑下一节的方法。
3.5 路径优化
由于A*寻路算法计算出的路径并没有把人的思维方式思考进去,所以角色的行走路线在玩家看起来会很奇怪,所走的轨迹是"折线形"的,在多个拐角处行走为"直走直转"形式,而常人的思维是在遇到多个拐角的地形会直接绕过这块,所走路线也是平缓的。
在计算机领域,专门研究曲线曲面方面的已经发展成计算机图形图像学的一部分,在对折线形地图(可看作折线形多边形)进行优化时,最为常用的方式就是用Bezier曲线(中文常称为贝塞尔曲线)去优化。使用Bezier曲线优化后的路径明显平滑很多,在一些大型地图中采用该曲线优化路径可以使路径更像人行走的路线,另外也有一些计算机研究人员指出Bezier曲线在优化路径的过程时,很多时候没有经过路径点,而这些路径点如果处于障碍物与可通行道路的边缘处,则可能优化后产生"穿过障碍物"的情况,所以采用了Catmull-Rom插值算法来优化路径,该算法的优点就是其计算生成的曲线经过所有的折线形路径的路径点。
3.6 分区域搜索优化
随着计算软硬件的快速发展,电子游戏场景中可以支持很大的地图,形成的网格可以达到千万甚至更高,而在这么大范围的地图中寻路,必然会产生发出寻路指令后,游戏角色会"卡顿"的现象,而CPU则要花费很多时间来执行寻路算法搜索路径。在很多游戏中会存在跨场景寻路,在进行寻路时要同时考虑好几张地图,每张地图的坐标又均是从(0,0)点或(0,0,0)开始生成的,用传统的优化方法对A*算法优化达不到效果。对于一些实时性要求很高的电子竞技游戏,寻路算法的效率要求会非常高,这个时候,应用智能寻路算法所找到的就不一定是最短路径,而是一定条件限制下的次优路径。
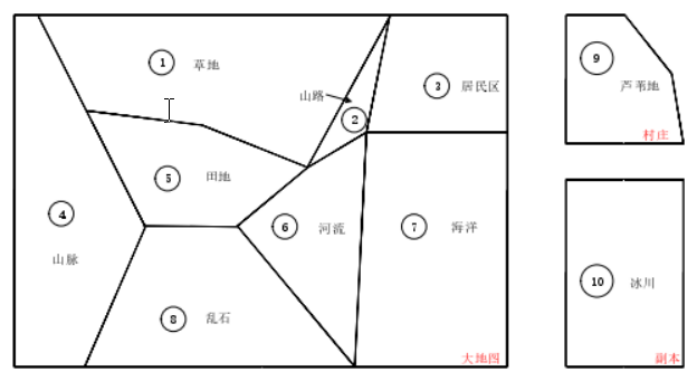
如上图,是一个复杂的地形图,共分为三个场景:大地图、村庄、副本。
首先对该地形图进行区域划分,图中已经大致划分好。在生成游戏地图的时候,地图上的信息是固定好的,所以可以给地图上的每个节点添加一个区域标记,不同的区域标记不同,同时每个区域的边缘会有几个特殊的点,这些点可能是两边的区域共同拥有的点。分区域寻路的具体步骤如下:
1)首先对生成的各场景地图进行标记,进行区域划分,不同地图的不同区域设置对应的权值。
2)对每个区域的边缘设置几个固定预搜索点(蓝色点),同时每个地图设置几个传送点(红色点),把这些点存入一个设置好的数据结构中,本文使用数组mapList存储。
3)确定好起始点S和目标点E,并把这两点加入数组mapList中。
4)建立一个无序数组Array,使用Dijkstra图算法搜索数组Array中的路径顺序(预搜索点包含"宏观"权值、区域标记等信息)。其中如果预搜索点传入本区域搜索信息,则只生成起始点到第一个预搜索点的路径,且第一个预搜索点设置为新的起始点。
5)对生成路径的每一条线段,起始路径和最后一条路径采用优化后的A*算法进行路径搜索,而剩余的每个区域的路径直接用第四步中的"宏观"路径进行替代。
6)合并第五步中的各路径,路径搜索完成,开始寻路。
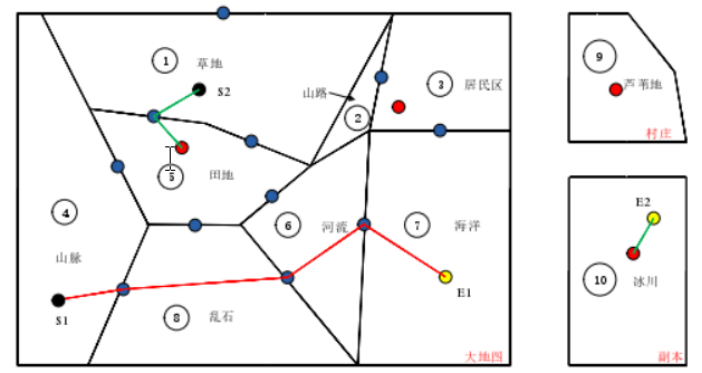
通过图中可以看出,有两次搜索过程,分别为S1-E1和S2-E2。对于S1-E1,首先通过计算得出行走路径经过的地形顺序为4-8-6-7,在使用Dijkstra算法计算出区域路径后,再使用优化过的A*算法在开始区域部分和结束区域部分的地形中进行改进后A*算法寻路,其余区域直接为两个蓝点间的距离,最终找到目标点,整个路径为图中红线部分。
四、A*寻路在游戏中的运用
到现在为止,看上去A*寻路只能用来计算起始点到目标点之间的最短路径,实际上,A*寻路的强大远不止于此。
在实际游戏中,很多时候,最短路径并不是最好的选择。需要寻路的AI角色可能是人 类、也可能是善于游泳的怪物、坦克或舰船,它要面对多变的地形,如可能是山地、森林, 也可能是沼泽、河流。每种AI角色都有自己的特点,可能很善于穿越某些地形,而对另一些 地形却束手无策或笨手笨脚。例如,一个人类士兵可以很容易地在森林中穿梭行走,而坦克就有一些困难;另外,最好也不要让坦克在山地上行驶,因为这样可能会暴露它的底部,使 它容易遭到攻击,而且坦克也不能急转弯。
还有一些情况下,我们希望AI角色能够避开强火力区域,选择更为安全的路线,或是为了进行伏击,选择迂回隐蔽的路线。为了让AI角色更聪明灵活,就需要用到战术寻路。
实现战术寻路的思路其实很简单,就是为不同区域赋予不同的代价值。前面说过,A*寻路的目标就是要寻找一条从起点到终点的总代价最小的路径,那么,要实现战术寻路,只需增加危险或闲难的区域(例如强火力区域或沼泽等)的代价值,A*就会尽量避开这些区域, 而选择更安全或容易的路径。
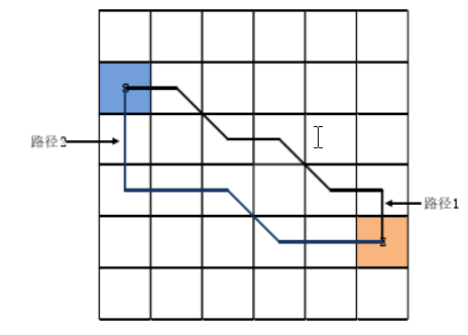
如下图所示,长方形物体表示墙,能够为AI角色提供火力遮挡。AI角色和玩家角色都存在于地图中并且可以远程射击,那么在寻路计算的同时可考虑以下战术寻路规则,完成AI寻路的目标。
规则1如果这条边的两个顶点都位于敌人火力攻击范围内,那么将这条边的行走代价加50;
规则2如果这条边只有一个顶点位于敌人火力攻击范围内,那么将这条边的行走代价加25;
规则3其他边的代价保持原值不变。
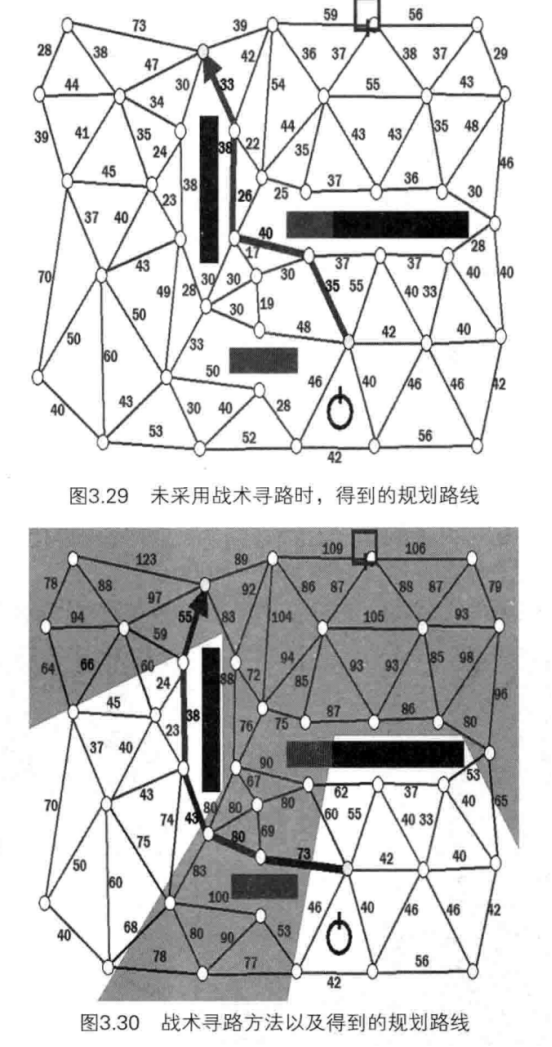
下图中的灰色区域表示敌人的火力攻击范围。与上面规则相应,两个顶点都在灰色区域 内的边满足规则1,只有一个顶点在灰色区域内的边满足规则2,而两个顶点都不在灰色区域 的那些边满足规则3。
为这些边赋予了新的行走代价之后,重新运行A*算法,这次得到的路径是图中黑色 较粗的曲线。可以看出,这条路径尽可能利用了障碍物的遮挡,尽量避开敌人的攻击火力区域。对于AI角色来说,这条新路径看上去比前面那条路径安全多了!
五、总结
本文主要研究方向是电子游戏中,人工智能中寻路系统里的智能寻路算法,角色在游戏场景中的地图上如何寻找到一条最佳路径或如何最快找到一条"次优"路径。本文先主要讲解了几种简单的图的搜索用到的算法,包括Dijkstra算法和最佳优先搜索算法。然后详细介绍了标准的A*算法及其原理。A*算法是游戏中最常用的寻路算法,但标准A*算法的效率并不能满足一些即时要求高的游戏的需要。针对寻路算法的分析和如何改进优化A*算法,本文进行了详细研究与剖析。
自从A*算法被提出来,人们不断的对其进行优化和扩展,进而衍生出一系列的A*衍生算法,比如最早用于火星探测机器人寻路的D*算法、控制最大搜索深度的Iterative Deepening A*算法、控制内存上界的Simplified Memory Bounded A*算法等。本文对标准的A*寻路算法进行了改进,优化了其启发函数,使用二叉堆维护开启列表,对地图中的权值做了优化处理,使A*算法的搜索效率更高;对经过计算生成的路径进行了贝塞尔曲线算法来使得路径更加平滑,使用分区域搜索方法来改进A*算法,使A*算法的应用性更高,同时满足特殊情况下的寻路要求。最后,本文介绍了寻路算法在游戏中的典型运用,设计了一个战术寻路规则作为案例。
参考文献:
- 冯俊翔,潘豪,谭世雨,李杨.A*算法的改进及其在移动端游戏中的运用.计算机光盘软件与应用, 2014
- 贾森浩.游戏人工智能中 A*算法的应用研究.杭州电子科技大学,2017
- 张永旭.基于路径搜索的改进A*算法研究.哈尔滨工程大学,2017
- 王功利,钟健麒.Unity3D射击游戏中人工智能与摄像机的运用.电子技术与软件工程.2017
- 赵振国.向量空间中A_算法的优化及应用.哈尔滨理工大学.2016
