3D数学与图形算法
坐标系
笛卡尔坐标系
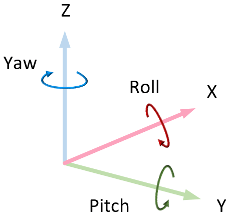
ue4 coordinate system
Roll(朝向)-Pich(右侧)-Yaw(纵轴)
- 使用左手坐标系的空间:模型空间、世界空间、裁剪空间、屏幕空间 等大部分我们常用的空间
- 右手坐标系空间:观察空间(摄像机)
向量
向量常用来表示点(坐标) 和 朝向(大小)
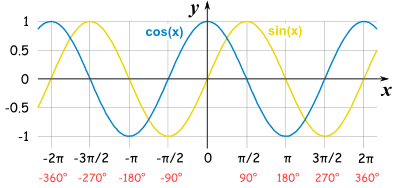
点乘:A*B = |A||B|cosθ
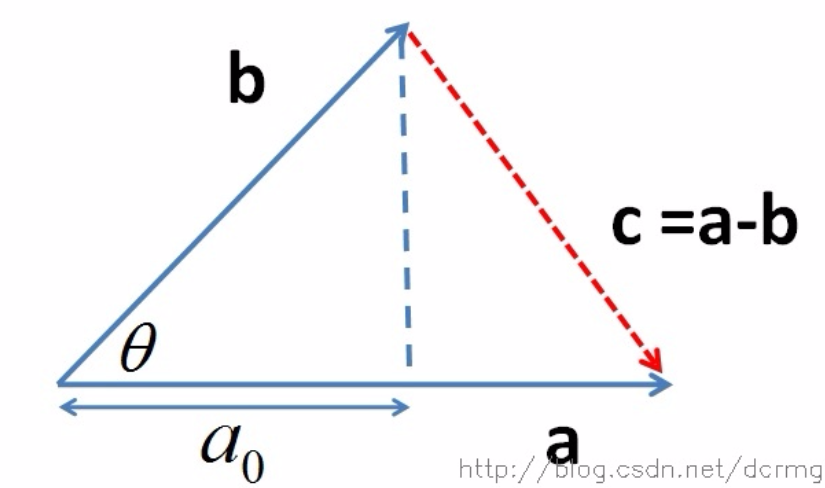
可用于计算cosθ以及b在a向量方向上的投影
其他作用:
- 计算敌人是否在自己身后:Forward * EnemyDir < 0
- b在a向量方向上的投影a0 = a*b / |a|² * a,长度为 |b|cosθ = a*b / |a|
- 计算离自己朝向角度最近的目标:cosθ = A*B = |A||B|,值越大越近
叉乘:a×b —— |a×b| = |a||b|sinθ
a × b = |a||b|sin(θ) * n(n 是一个与 a 和 b 都垂直的单位向量)
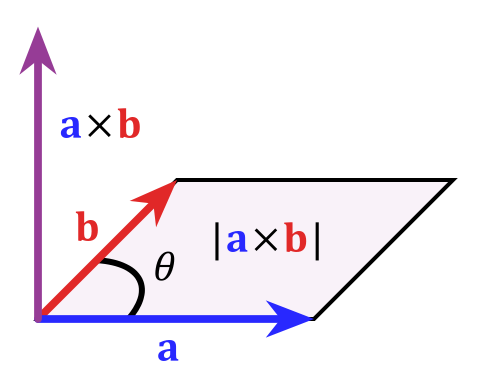
通常用于生成"法向量"。右手定则指的是:当你将右手的食指指向 a,中指指向 b 时,大拇指所指的方向就是 a × b 的方向。
图中同时包括 二维叉乘(面积) 与 三维叉乘(坐标系) 的结果
其他作用:
- 计算最小的旋转角度。比如做一个方向盘,当前OA,目标点到OB,可以OA×OB,使用右手定则,z分量大于0逆时针旋转,小于0顺时针(点乘也可以做到)
- 计算目标在自己的左右方位:(Forward × ToTarget).y > 0 右侧。因为y分量>0表示在正平面,也就是sinθ>0,表示0~180°;而y分量<0在负平面,表示-180°~0
矩阵
- 表示3D空间信息(Transform)
- 缩放变换,旋转变换,扩展平移变换
矩阵,常用来 变换,或用于表示 变换(Transform)
缩放,只需要三维的变换矩阵:
[a, 0, 0][0, b, 0][0, 0, c] 坐标乘以该矩阵后即得到缩放后的坐标
旋转,同样只需要三维,以绕Y轴旋转为例:
[ cosθ, 0, sinθ][ 0, 1, 0][-sinθ, 0, cosθ] x,z轴类似,绕任意轴也同样可以在三维内实现
平移,则需要4x4四维矩阵与扩展为四维向量(w=1的齐次坐标)后的三维坐标运算:
[1, 0, 0, tx] [x] [x+tx][0, 1, 0, ty] * [y] = [y+ty][0, 0, 0, tz] [z] [z+tz][0, 0, 0, 1] [1] [ 1 ]
原理就是 矩阵的乘法原理:
若

为

矩阵,

为

矩阵,则他们的乘积

(有时记做

)会是一个

矩阵。其元素计算方式为:

以 3×3 与 3×3 方阵相乘为例:
[a11, a12, a13] [b11, b12, b13] [a11(b11, b12, b13) + a12(b21, b22, b23) + a13(b31, b32, b33)] [a11b11 + a12b21 + a13b31, a11b12 + a12b22 + a13b32, a11b13 + a12b23 + a13b33][a21, a22, a23] * [b21, b22, b23] = [a21(b11, b12, b13) + a22(b21, b22, b23) + a23(b31, b32, b33)] = [a21b11 + a22b21 + a23b31, a21b12 + a22b22 + a23b32, a21b13 + a22b23 + a23b33][a31, a32, a33] [b31, b32, b33] [a31(b11, b12, b13) + a32(b21, b22, b23) + a33(b31, b32, b33)] [a31b11 + a32b21 + a33b31, a31b12 + a32b22 + a33b32, a31b13 + a32b23 + a33b33]
具体示例:

简言之就是拿 A的横向元素 乘 B的纵向横列元素、再加起来... 得到一个结果和
方位角
旋转有3种表示方法:欧拉角,矩阵,四元数。各有优势
一般来说四元数最适合引擎运算,其是通过相似矩阵来实现旋转变换的,功效接近于三维旋转矩阵
q = (x, y, z, w) = xi + yj + zk + w
坐标空间
MVP矩阵(Model-View-Projection Matrix) 将顶点从模型空间变换到观察空间
模型空间->世界空间
用复合变换 Pworld = Mmodel * Pmodel
世界空间->观察空间
得到将相机变换到坐标轴原点的逆矩阵,且因变换为右手坐标系,需要对z分量取反
Pview = Mview * Pworld
观察空间->裁剪空间 及视锥体剔除:
- 如果是透视投影,需要视锥体6个裁剪平面,重点依据近剪裁平面、远剪裁平面。根据FOV改变视野张开角度,计算出远近裁剪平面的高度,再由横纵比Aspect得到宽度 =2*near/far*tan(FOV/2)。由此得到投影矩阵 Pclip = Mfrustum * Pview。还 可以根据±w分量,得到判断变换后的顶点是否位于视锥体内的不等式。
- 如果是正交投影,则因为near=far,计算简单很多,w分量仍然是1
裁剪空间->屏幕空间:
- 齐次除法:用w分量除以xyz分量。使透视投影的裁剪空间变为一个长度为1的单位立方体,转化为 归一化设备坐标NDC。
- 再用屏幕映射公式得到ScreenX,Y。Z分量用于深度缓冲
基本图形生成算法
OpenGL图形学
画线算法:如根据直线方程 y=kx+a
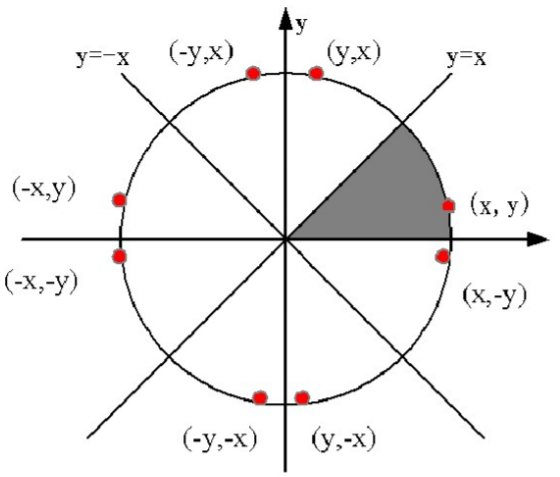
画圆算法:△x=1,计算最逼近的y像素....只需要推出1/8圆的坐标,就可以推出整个圆的
中点画椭圆算法:先画1/4椭圆
区域填充算法:判断点在区域内外【 将该点与多边形各顶点连线,若角度和=0,则为外点,若和=360°,则为内点】【射线法检验交点数为偶数则在区域外】
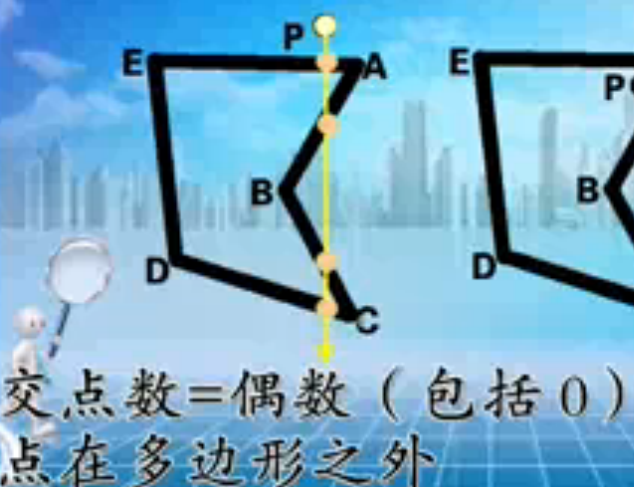
扫描线填充算法 / 边填充算法 / 种子填充算法
字符算法:点阵存储
曲线曲面算法
Bézier曲线
B样条曲线
碰撞检测
求交算法
点与直线求交:从点连纵轴与直线夹角计算即可
点与三角形求交:交点计数法 / 夹角之和法 / 代入三直线法 / 叉乘法(高效):连线得3个向量PA, PB, PC,两两叉乘 a×b = x1y2-x2y1,如果三个结果都是同号的(可以判断出点在哪一侧),就在内
点与多边形求交:扫描线求交点,角度和2π(通过atan来算),叉积法也可判断是否在多边形各边内侧
直线与直线交点:解二元一次方程组
直线与平面交点:通过法向量
直线与圆交点:计算到圆心的距离。。
点与AABB:两端点即可
AABB与AABB:基于每一条坐标轴 并利用面的边缘去检测,比如x轴是否会重叠

球与球:r1+r2
球与AABB:计算AABB最近的点(不一定是一个顶点)和球体的中心之间的distance与r
消隐算法
画家算法:由远及近地绘制各面,相当于消除隐藏面
Z-buffer缓冲区算法:保存每个像素与视点的距离,渲染更靠前的
区间扫描线算法:最快,算法优点是将像素计算改为逐段计算,效率大大提高
裁剪算法
直线段裁剪:编码算法,中点分割法,参数化裁剪方法,梁友栋算法
多边形裁剪
字符裁剪
Unity旋转、平移
